MIXING & EFFECTS
Fruity Formula Controller
Fruity Formula Controller generates automation control data based on user-defined formulae. It can be used for boolean (true or false) operations, like creating logic gates and conditional statements, where the output is dependent on the state of the variable(s). The Formula Controller will appear as a Formula ctrl - Out option in the Link dialog. It is just one of the many internal automation controllers available in FL Studio.
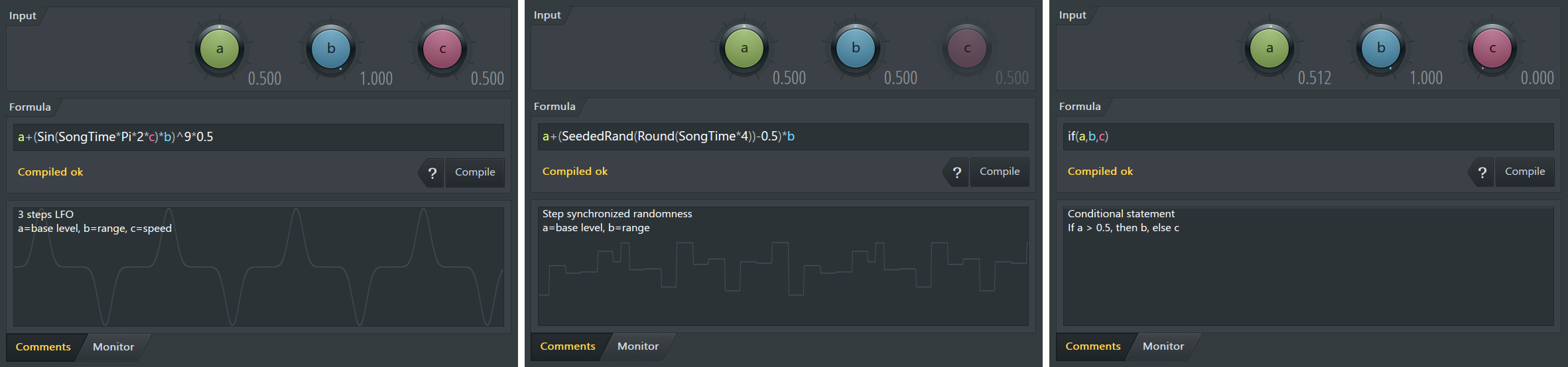
How to use:
- Load Fruity Formula Controller in a Mixer FX Slot. NOTE: Renaming the Formula Controller will help you find the correct automation source when more than one is used in a project.
- Enter a formula or select one from the plugin presets and make sure it compiles correctly.
- Link the target Synth, Effect or FL Studio interface control to the 'Formula ctrl - Out' option (or custom name used at step 1) from the Link Dialog > 'Link assignment' menu.
- Link other internal or external hardware controllers to variables A, B and C OR record A, B, C tweaks in real-time as the project is playing.
- Alternatively, Fruity Formula Controller can be routed in Patcher.
Video Tutorials
Parameters
- a/b/c - These knobs are the parameters, that can be used as variables in your formulas. Enter them into your formula as a, b and c variables (see the list of operators and functions below).
- Formula - This is where you enter your formula. Press ENTER or Compile to compile a formula. If the formula is a valid mathematical expression, you will see a message 'Compiled ok' below the formula. If it's not, you will see a helpful error message. NOTE: The output of the formula must range between 0 to 1 in order to qualify as valid control data, values outside of that will be cut off. (see below).
- ? - Opens the Syntax, Objects and Functions table (see below).
- Compile - Compiles the formula. Alternatively press ENTER when using the formula edit box.
- Comments - Type comments here. If text exceeds the height of the window a scroll-bar will appear on the right side. Supports RTF text from WordPad. The formula Monitor graph also displays behind the text for your convenience.
- Monitor - Shows the output from the formula in real-time. NOTE: Many formulas will not display as a moving trace until you click Play on FL Studio's transport panel.
Syntax, Objects & Functions
The following syntax, functions and objects are supported by the Formula Controller:
| Operators | ||
|---|---|---|
| Abbreviation | Description | Example |
| + | addition | a+b |
| * | multiplication | a*b |
| - | subtraction | a-b |
| / | division | a/b |
| ^ | power | a^b |
| = | comparison, equal | a=b |
| in | same as = | a in b |
| <> | not equal | a=b |
| > | greater than | a>b |
| >= | greater than or equal | a>=b |
| <= | lesser than or equal | a<=b |
| < | lesser than | a<b |
| % | converts percentages into decimal values | Value% |
| ! | factorial, returns the scalar part of a | a!*b |
| div | integer divide | Numerator div Denominator |
| mod | modulo, returns the remainder of a/b | a mod b |
| fmod | floating point modulo | a mod b |
| not | logical not, returns 1 when a <= 0.5 and 0 when a > 0.5 | not a |
| or | logical or, returns 1 when a or b or both are > 0.5 | a or b |
| and | logical and, returns 1 when both a and b are > 0.5 | a and b |
| xor | logical xor, returns 1 when a or b is > 0.5 | a xor b |
| shr | integer shift bits right (divide), equivalent to x/2^y | Value shr Amount |
| shl | integer shift bits left (multiply), equivalent to x*2^y | Value shl Amount |
| Functions | ||
| Abs | absolute, flips the negative part of an output into positive | Abs(a) |
| ArcCos | inverse cosine | ArcCos(a) |
| ArcCosh | hyperbolic inverse cosine | ArcCos(a) |
| ArcSin | inverse sine | ArcSin(a) |
| ArcTg | antitangent | ArcTg(a) |
| ArcTanh | hyperbolic inverse tangent | ArcTg(a) |
| ATan2 | arctangent angle/quadrant of a given number | Atan2(a,b) |
| Case | returns b if a=1, else returns c | Case(a,b,c) |
| Cos | cosine | Cos(a) |
| Cosh | hyperbolic cosine | Cos(a) |
| CoSec | cosecant | CoSec(a) |
| DegToRad | convert degree value to radians | DegToRad(a) |
| Ceil | rounds up to nearest integer | Ceil(a) |
| Ctg | cotangent | Ctg(a) |
| Exp | exponential | Exp(a) |
| Floor | rounds down to nearest integer, same as Int | Floor(a) |
| Fold | wave folding operation | Fold(a) |
| Frac | fractional part | Frac(a) |
| GetTempo | returns current project tempo | GetTempo |
| If | if a > 0.5 then b, else c | if(a,b,c) |
| IfE | returns 1 if a=b | IfE(a,b) |
| IfG | returns 1 if a>b | IfG(a,b) |
| IfGE | returns 1 if a>=b | IfGE(a,b) |
| IfL | returns 1 if a<b | IfL(a,b) |
| IfLE | returns 1 if a<=b | IfLE(a,b) |
| Int | integral part | Int(a) |
| Inter | returns 1 if a > b and a < c. If c < b, b & c values will be swapped| Inter(a,b,c) |
|
| Internoswap | as Inter but doesn't swap a & b | Internoswap(a,b,c) |
| Intpower | integer power, Value^Power | Intpower(Value, Power) |
| Ln | logarithm base e | Ln(a) |
| Log10 | logarithm base 10 | Log10(a) |
| Log2 | logarithm base 2 | Log2(a) |
| LogN | logarithm a is the base, b is the number to calculate from | LogN(a,b) |
| Map | maps the value a into the range b..c, equivalent to x * (z - y) + y | Map(a,b,c) |
| Max | maximum, returns the greater input | Max(a,b) |
| Min | minimum, returns the lesser input | Min(a,b) |
| Neg | negative | Neg(a) |
| Pi | returns the value of pi | Pi |
| Power | floating point power, a^b | Power(a,b) |
| Pow | floating point power, a^b | Pow(a,b) |
| RadToDeg | convert radian value to degrees | RadToDeg(a) |
| Rand | outputs continuous random values (0..1) | Rand |
| Round | round to nearest integer | Round(a) |
| Sec | secant | Sec(a) |
| SeededRand | static random value (0..1), changes when seed is changed | SeededRand(Seed) |
| Sin | sine | Sin(a) |
| Sinh | hyperbolic sine | Sinh(a) |
| Sqrt | square root | Sqrt(a) |
| Sqr | square (same as a^2) | Sqr(a) |
| Sum | sum of arguments | Sum(a,b) |
| Tg | tangent | Tg(a) |
| Tan | tangent | Tan(a) |
| Tanh | hyperbolic tangent | Tanh(a) |
| Trunc | truncate, limits the number of digits right of the decimal point | Trunc(Value) |
| Warp | warps signal a around to warp point b | Warp(a,b) |
| Special (FL Studio-related) | ||
| a | value of knob A | a |
| b | value of knob B | b |
| c | value of knob C | c |
| SongTime | song position, in quarters | SongTime() |
| Time | system time, in ms | Time() |
| Tension | Curves the line, positive or negtively depending on sign | Tension(Value,Rate of change) |
| Gadgets | ||
| Date | system date | Date() |
| MouseX | mouse cursor X position | MouseX() |
| MouseY | mouse cursor Y position | MouseY() |
Output
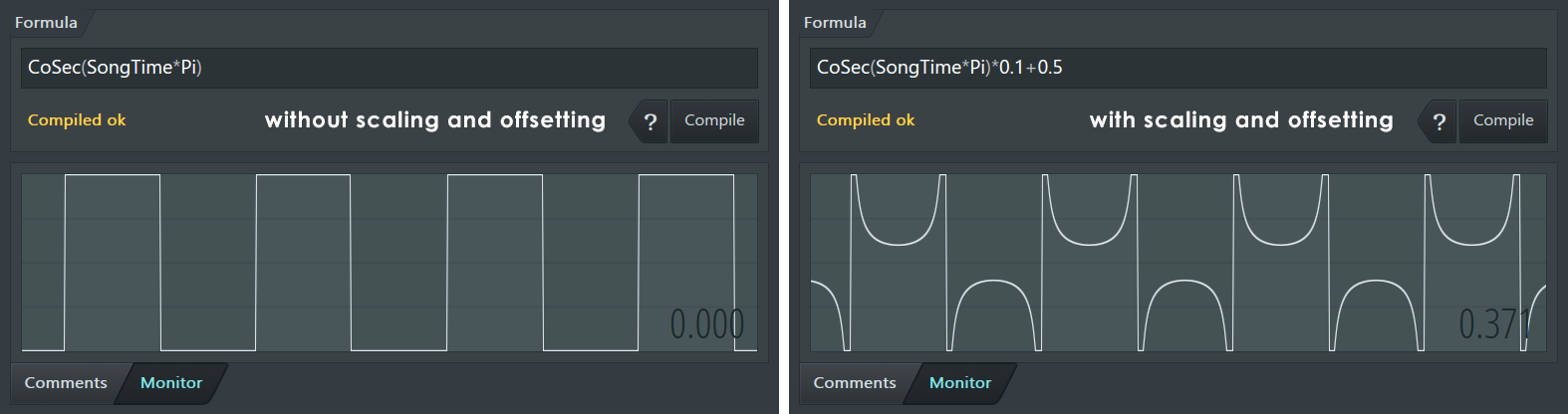
Fruity Formula Controller can only output values that are within the range of 0 to 1, values outside of this range will be calculated, but not visible in the Monitor view. For certain functions, there's a wider range of potential output values outside of the visible range, which can be useful for intermediate steps of the calculation (i.e. before the final output value). For example, the CoSec() -function by definition has a range of y≤−1 or y≥1, which means all real numbers except those in between -1 and 1. In the image below, the CoSec() -function has been resized (multiplied with a small number) to display a wider range in the output. There are also functions that only return integers, which means that without scaling they only appear to return either 1 or 0.
Manipulating Functions
Sine Function Example
Let's examine the formula 0.5*Sin(SongTime*Pi*2+0.25)+0.5, which outputs a sine wave. Below the formula has been broken down into individual components, described as A - amplitude multiplier, F - frequency multiplier, O - offset and P - phase offset.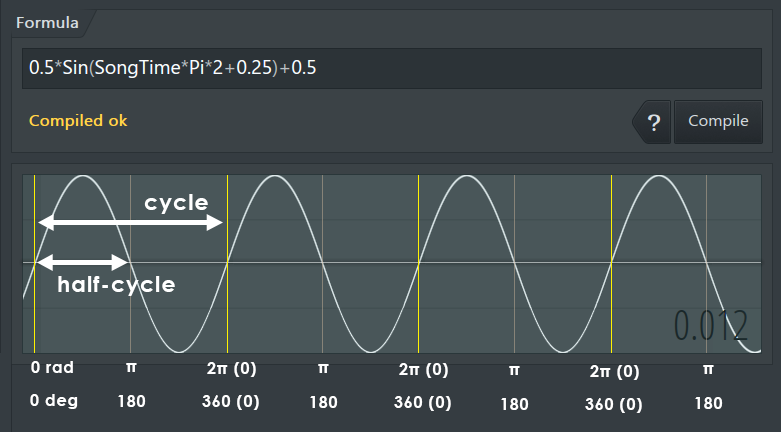
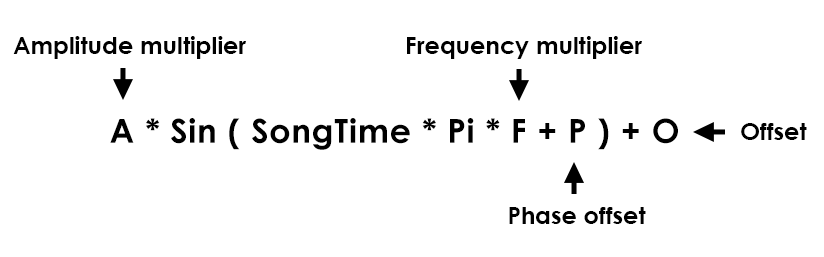
- Multiplication/division outside of the function (A) scales the amplitude of the output.
- Multiplication/division inside of the function (F) scales the frequency of the output. A higher scalar value outputs a higher frequency.
- Addition/subtraction outside of the function (O) offsets the output (moves it up or down).
- Addition/subtraction inside of the function (P) offsets the starting phase of the output (moves it left or right).
- To observe a moving trace, SongTime or Time must be used inside of the function, or alternatively any changing control data from outside of the Formula Controller connected to one of the variables.
- Multiplying SongTime with a multiple of Pi makes the resulting waveform fit evenly into the length of a pattern. Pi represents half a cycle in radians, and 2*Pi represents a complete cycle. A sine wave is shaped symmetrically in every half cycle period. In order for the output to keep repeating a complete half cycle, the frequency must be scaled by a multiple of pi. Example: 0.5*Sin(SongTime*Pi*(Int(b*10))) + 0.5 creates a sine wave, where parameter b adjusts the frequency. The Int() -function is used to transform b into integer values, so that the frequency can only be changed in half cycle increments (Pi * integer).
Example Formulas
Here is a collection of example formulas. If after copying and pasting into Fruity Formula Controller the output is stuck at 0, make sure parameters a, b and c are not all set to zero, and that you pressed Compile or ENTER key. Formulas that use SongTime will require Song/Pattern to be playing. Some results may at first look unexpected, depending on the positions of the parameters (adjust them and see what happens).
| Basic Waveforms | ||
|---|---|---|
| Name | Description | Formula |
| Sine | basic sine wave | 0.5*Sin(SongTime*Pi)+0.5 |
| Sine | sine wave with an adjustable amplitude, frequency and offset | a*Sin(SongTime*Pi*b)+c |
| Sine | as above, but the frequency has discrete values | a*Sin(SongTime*Pi*(Int(b*10)))+c |
| Sine | sine wave with an adjustable amplitude, initial phase and offset | a*Sin(SongTime*Pi+b*Pi)+c |
| Triangle | basic triangle wave | 0.319*ArcCos(Cos(SongTime*Pi)) |
| Triangle | triangle wave with an adjustable amplitude, frequency and offset | a*ArcCos(Cos(SongTime*Pi*2*b))+c |
| Triangle | as above, but the frequency has discrete values | a*ArcCos(Cos(SongTime*Pi*(Int(b*10))))+c |
| Triangle | triangle with an adjustable amplitude, initial phase and offset | a*ArcCos(Cos(SongTime*Pi+b*Pi))+c |
| Sawtooth | basic sawtooth | Frac(SongTime) |
| Sawtooth | sawtooth with an adjustable amplitude, frequency and offset | a*Frac(SongTime*b*2)+c |
| Sawtooth | as above, but the frequency has discrete values | a*Frac(SongTime*0.5*Int(b*10))+c |
| Sawtooth | sawtooth with an adjustable direction | Abs(Round(a)-Frac(SongTime)) |
| Square | basic square with 50% duty cycle | Round(Frac(SongTime)) |
| Square | basic square with 50% duty cycle (using a sine function) | Round(0.5*Sin(SongTime*Pi*2)+0.5) |
| Square | square with an adjustable amplitude, frequency and offset | a*Round(0.5*Sin(SongTime*Pi*2*b)+0.5)+c |
| Square | as above, but the frequency has discrete values | a*Round(0.5*Sin(SongTime*Pi*(Int(b*10)))+0.5)+c |
| Pulse | square with an adjustable pulse width | Round(0.5*Sin(SongTime*Pi)+a) |
| Pulse | square with an adjustable amplitude, frequency and pulse width | a*Round(Frac(SongTime*2*b)+0.5-c) |
| Sample and hold | random output with adjustable amplitude, frequency and offset | b*SeededRand(Int(SongTime*a))+c |
| Miscellaneous | ||
| Distorted Sine | Slightly distorted sine with an adjustable frequency | Pi/5*ArcTg(Sin(SongTime*2*Pi*b))+0.5 |
| Rectified Sine | Half-wave rectified sine with an adjustable frequency | Sin(SongTime*Pi*b) |
| Rectified Sine | Full-wave rectified sine with an adjustable amplitude and frequency | a*Abs(Sin(SongTime*Pi*b)) |
| Cones | Non-linear triangular shape with an adjustable amplitude, frequency and offset | a*ArcTg(cos(SongTime*Pi*b)-Sec(SongTime*Pi*b))^2+c |
| Eggs | Half-circle like shape with an adjustable amplitude, frequency and offset | a*(0.5+0.5*Cos(SongTime*Pi*b+Pi))^(1/5)+c |
| Boolean Operations | ||
| Buffer | input equal to the output | a |
| NOT | inverse of buffer | 1-a |
| AND | both a and b must be 1 to return 1 | a*b |
| OR | either a, b or both must be 1 to return 1 | a+b |
| XOR | exclusive or, either a or b must be 1 to return 1 | (a+b)=1 |
| NAND | inverse of and | 1-(a*b) |
| NOR | inverse of or | (a+b)=0 |
| XNOR | inverse of xor | a=b |
NOTE: Boolean operations will behave correctly when using boolean values, either 1 or 0 (true or false). The operators used are regular arithmetic operators and may output different results with other types of values.
Plugin Credits: Didier Dambrin, Andrew Tumashinov (RapidEvaluator)